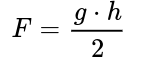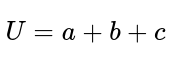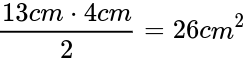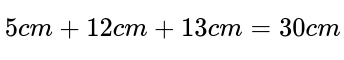Flatarmál og ummál þríhyrnings
Flatarmál þríhyrnings er fengið með því að margfalda grunnlínu og hæð þríhyrningsins og deila svo með tveimur.
Flatarmál rétthyrnings er einfalt að reikna (lengd * breidd) og við getum skipt rétthyrningi í tvo jafnstóra þríhyrninga með einfaldri skálínu horn í horn. Flatarmál annars þríhyrningsins er þá jafnt og hálft flatarmál rétthyrningsins eða flatarmál rétthyrningsins deilt með 2. Flatarmál hins er það sama. Þannig má hugsa þríhyrning sem hálfan rétthyrning.
Ummál þríhyrnings er fengið með því að leggja saman allar hliðarlengdir þríhyrningsins.
Hér kemur hæð þríhyrningsin ekki málinu við, hæð þríhyrningsins getur samt verið sú sama og hliðarlengd, en einfaldast er að hugsa ummál einungis sem summu hliðarlengda.
Sýnidæmi
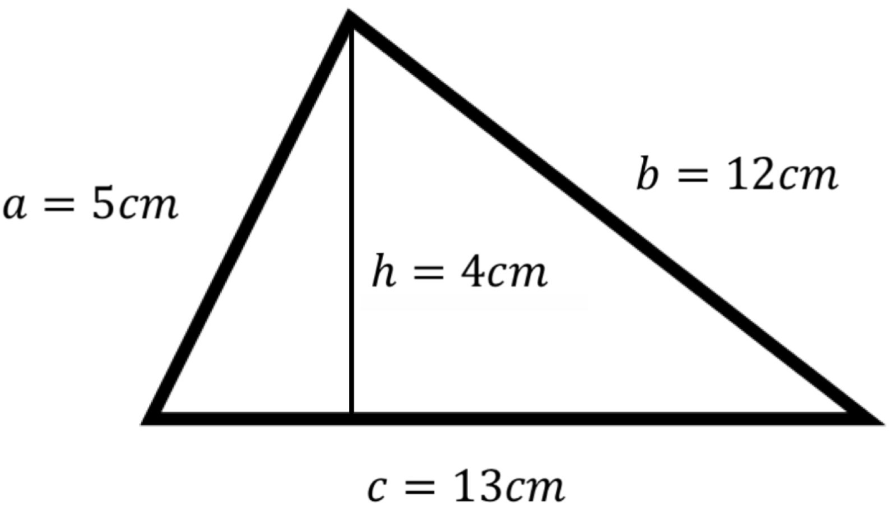
Hér til hliðar er þríhyrningur með hliðarlengdirnar 5 sentimetrar, 12 sentimetrar og 13 sentimetrar, og hæðina 4 sentimetrar.
Hvernig er fundið flatarmál þríhyrningsins?
Á myndinni er okkur gefin hæðin 4 sentimetra ef að við notum línu c sem grunnlínu (13 sentimetrar). Getum við því sett þær lengdir inn í formúluna fyrir flatarmál þríhyrnings. 4 sentimetrar sinnum 13 sentimetrar deilt með 2 eru 26 fersentimetrar.
Hvernig er fundið ummál þríhyrningsins?
Þegar við finnum ummál leggjum við saman allar hliðarlengdir þríhyrningsins. Ummálið er því 30 sentimetrar.
Hér pössum við okkur á að leggja ekki hæðina við, enda kemur hún ummálinu ekki við.